エクセルで簡単にデータ分析【コロナのデータで解説】
データ分析をしたい人

初心者でも、エクセルで簡単にデータ分析することはできませんか?データの相関をしりたい。回帰式を取り入れてデータ分析してみたい。
こういった疑問を解決します。
ポイント
- 1.エクセルで簡単にデータ分析をする方法
- 2.エクセルで簡単にデータ分析をするときの便利な情報
私は東証一部上場企業で10年間データ分析を経験しました。今は日本の大手データ分析企業と一緒に仕事をしています。
1.エクセルで簡単にデータ分析をする方法
以下の3つのステップで説明します。
「データ用意」→「データ基礎調査」→「応用して回帰線で相関を見る・予測する」
1-1.データを用意する
データを用意する。データが無いものはデータ分析ができません。
今回、東京都のオープンデータを利用して、そのデータから基礎分析をします。
東京都オープンデータはここです→https://portal.data.metro.tokyo.lg.jp/
新型コロナウイルスの陽性患者発表のCSVをダウンロードして使います。※2020/05/04のAM時点のデータを利用しています。
上記、赤枠をクリックすると以下のデータが取得できます。
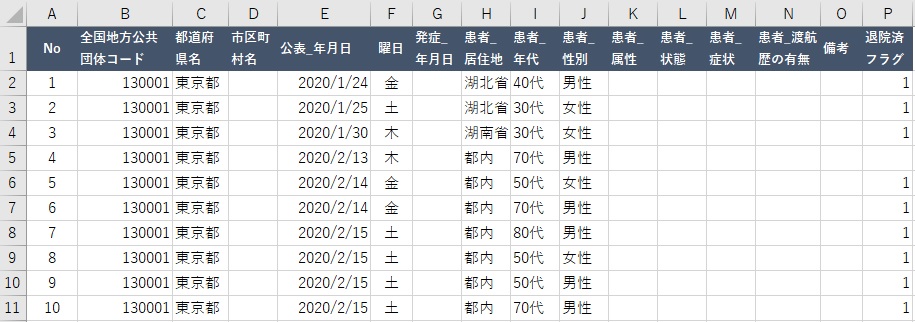
他に分析したいデータがあれば、そちらをご活用ください。
まずはデータを用意しましょう。
1-2.データの基礎調査をする
まずは、データの基礎調査をします。基礎がとっても重要です。
正しく項目の定義を知らぬまま対応をすると、後戻りが発生して非効率 かつ 誤った情報提供をする可能性が高まります。
単項目→グラフで可視化→クロス集計といった3ステップで説明します。
(1)単項目の中身を確認する
エクセルのピポット機能を使って1列(1項目)に何の値が何件入っているかを見ます。
不必要なデータ項目を洗い出すためでもあります。
今回は、6項目の傾向を見ました。
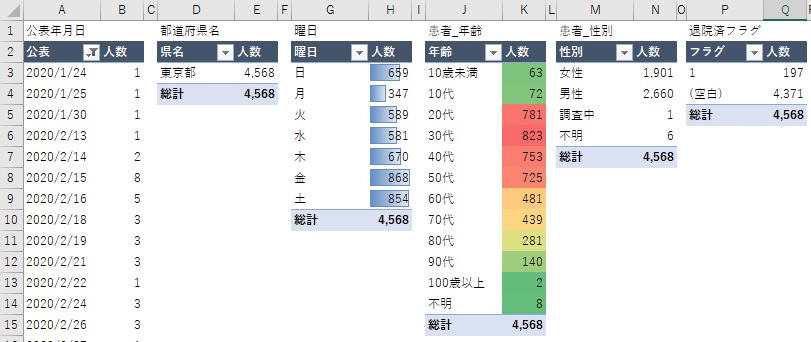
特にカラーバーは数字を読まずとも視覚的に傾向が分かるので、重宝しています。
Q:ピポットテーブルを作るには?
A:CSVデータのセルを選択した状態で「挿入」→「ピポットテーブル」
Q:数字にデータバーやカラースケールを入れるには?
A:「ホーム」→「条件付き書式」
ここで、データに傾向が見られない、調査したいデータ要因と違うものは、データ分析から「除外」しましょう。
不要な項目が多くあると分析効率が悪いためです。
除外した項目は「都道府県名」「曜日」です。
理由は、
都道府県名:東京都しかないから(データ傾向が見られない)
曜日:検査機関の稼働日の影響を多く受けるため(調査したいデータ要因と違うものが含まれる)
ただし、除外項目も、求める仮説がしっかりあるのであれば使っても良いと思います。
このように、まずは、単項目の中身を確認します。
(2)さらにグラフなどで可視化
公表年月日をグラフで可視化します。
数字の羅列よりもグラフで視覚的に表現した方が分かりやすいからです。

Q:グラフを作るには?
A:ピポットを選択した状態で、「挿入」→「グラフ」
多忙な経営者や上位者などに報告するときには、考える時間を短縮するため、一目で状況を分かりやすく伝えるのが良いです。以下のように、粒度を荒くして7日の週単位でグループ化すると見やすくなります。
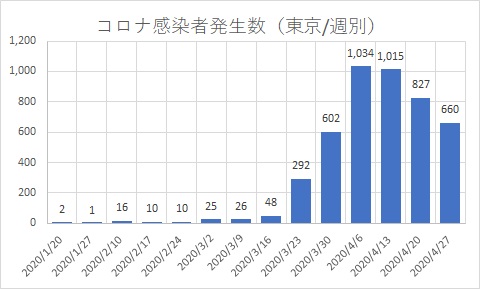
今回は棒グラフしか使いませんでしたが、円グラフや折れ線グラフなども、分かりやすく伝えましょう。
グラフで可視化して傾向をみます。
こんなかたちで見ていくと、使えそうな項目が4項目あることがわかりました。
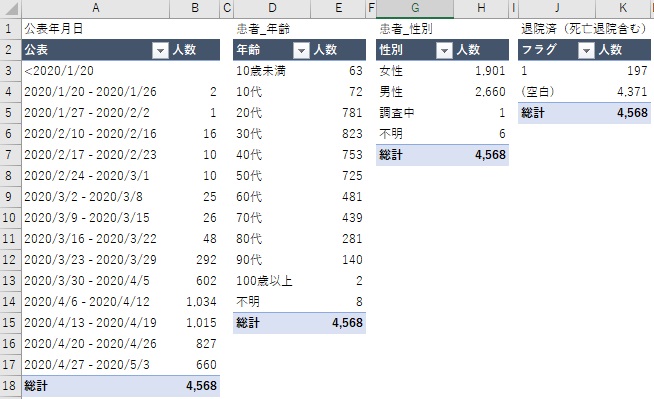
(3)次にクロス集計をする
次に関係がありそうな2軸の項目でクロスして集計します。
軸を増やすことでより細かな分析ができます。
以下、縦軸が「公表年月日」、横軸が「年齢」のクロスした集計になります。
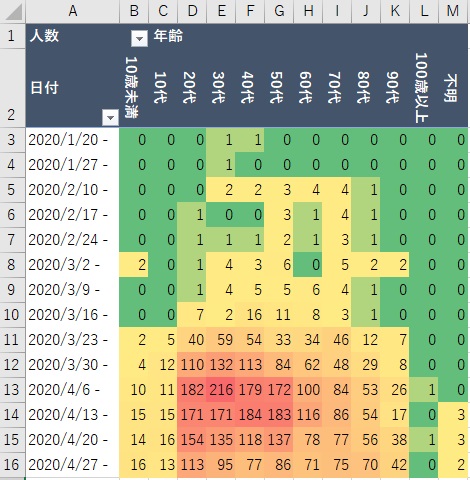
ここから分かることは
・3月23日週から20~50代を中心に増加
・4月6日週がピークになっており、特に30代が一番多い
などです。
規模だけでなく、週ごとの構成比もみてみましょう。
なぜなら、規模だけでは分からない、傾向が見えてくることがあるためです。
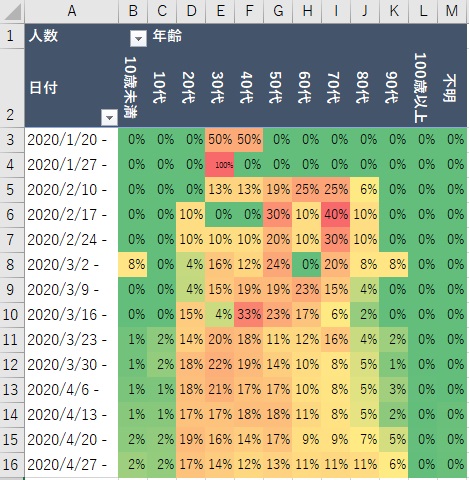
ここから分かることは
・直近は若年層20~50代の割合が減少。一方で60代以上の割合は上昇。
などです。
3軸以上では見ないの?と考える方もいると思いますが、目的変数(求めたいゴール)が何か決まってない状態では、3軸にしたところで迷走するだけです。
関係がありそうな項目どうしは2軸の項目でクロスして集計しましょう。
1-3.応用して散布図で相関を見る・予測する
最後に応用編です。今までの基礎情報を使って「散布図で相関を見る」と「予測する」を解説します。
(1)散布図で相関をみる
散布図とは、エクセルで用意されているグラフの一つです。
相関とは、二つ以上の事物の比例や反比例といったように、互いに影響を持つことです。一方が変われば他方もそれに合わせて変わること、あるものの影響を受けて関わり合っていることです。
これが分かると、物事の関係が数字でわかりやすく理解することができます。
具体例を示します。年齢別に患者フラグ率を見た具体例を示します。
患者フラグ率とは「患者数」に占める「退院済フラグ(死亡退院含む)」の割合です。ちなみに、「退院済フラグ(死亡退院含む)」197人ですが、現時点で東京都発表の検査陽性者の状況(東京都)では死亡された方が145人存在するため、退院済フラグのうち、75%程度と大多数が死亡に含まれるのではないかと想定しています。※もし認識違いがありましたら申し訳ございません。
縦軸が「患者フラグ率」、横軸が「年齢」です
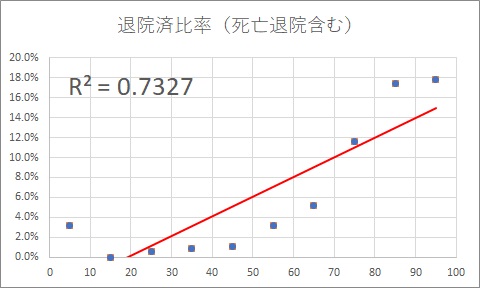
ここから分かったこと
年齢が上がるごとに正の相関が見えます。70代で10%超しています。
相関係数:R2=0.73 =「強い相関あり」です。
Q:グラフの散布図はどこにあるの?
A:2列の数字データを選択→「挿入」→「散布図」
Q:グラフにある線を出すには?
A:点を右クリック→「近似曲線の追加」
Q:R2(相関係数)を表示するのは?
A:線を右クリック→「近似曲線の書式設定」→「グラフにR-2乗値を表示する」をチェック
相関係数は
| 相関係数 | 相関の強さ |
| 0.0~±0.2 | ほとんど相関がない |
| ±0.2~±0.4 | 弱い相関がある |
| ±0.4~±0.7 | 相関がある |
| ±0.7~±0.9 | 強い相関がある |
| ±0.9~±1.0 | ほぼ完全な相関がある |
と言われています。
次に、多項式近似(回帰曲線)でも見てみます。
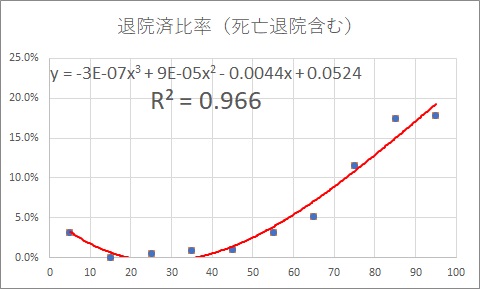
ここから分かったこと
相関係数:R2=0.96 =「ほぼ完ぺきな相関あり」です。
Q:多項式近似はどう表示するの?
A:線を右クリック→「近似曲線の書式設定」→「多項式近似」にチェック
Q:グラフの数式を表示するには?
A:線を右クリック→「近似曲線の書式設定」→「グラフに数式を表示する」をチェック
計算式を出すことで、自分の年齢に対してフラグ率が計算で求めることもできます。
定義しているデータでは回帰を使うまでもないのですが、回帰線での相関、計算式を作ることができました。
(2)予測する
コロナの感染者数がいつ収束するのか?
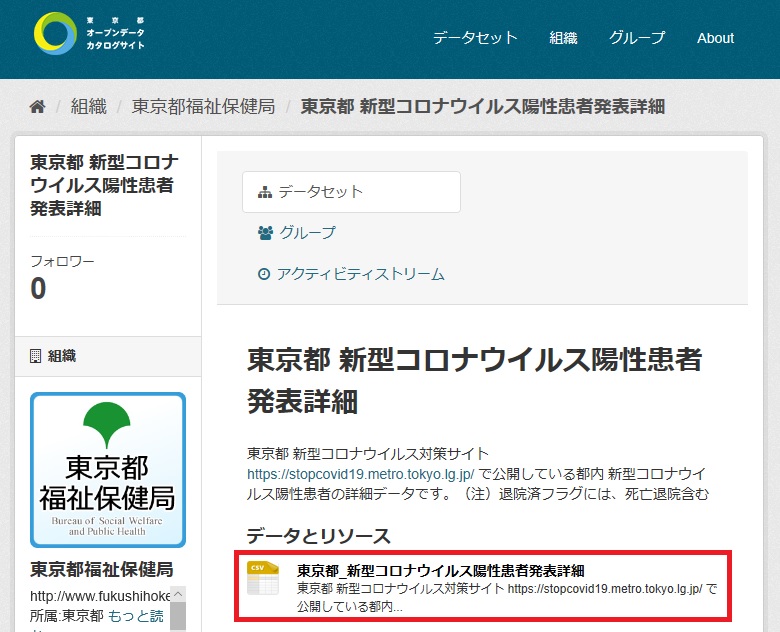
4月の4週の推移をもとに、5月以降をTREND関数を使って数字を出してグラフにしました。
青色が実績で、赤色が予測です。

4月並みに自粛を続ければ、6月8日週には感染0になるという予測も表すことができます。※あくまで4月並みに自粛を続ければ。
Q:なぜTREND関数なのか?
A:重回帰分析で予測できるから。単に傾向を見るのであれば前の散布図から回帰でもOK
予測にはもっと重要な要素があるよ。という声もあると思いますが、大きな傾向を見るのであれば、このような単純な予測でも当たることもあります。
また、それが間違いであっても、指標がない未来より、指標を作って対策する未来の方が良いと考えます。
散布図で相関を見る。予測を作ってみましょう。
(3)番外編_東京都人口と対比してみました
東京の人口を別途取得※1してコロナ患者数の割合をみると、
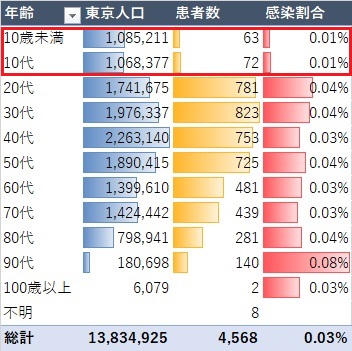
10代以下の感染割合が特に少ないことも分かります。
エクセルで簡単にデータ分析をするときの便利な情報
参考になるデータサイト
データ比較に有益な情報が載っています。
データカタログサイト:https://www.data.go.jp/
統計局の統計データ:http://www.stat.go.jp/data/
東京都の統計※1:https://www.toukei.metro.tokyo.lg.jp/
気象庁の気温情報:https://www.data.jma.go.jp/obd/stats/etrn/index.php
エクセル上級者を真似よう
報告がうまい人、分析がうまい人の方法を真似るのが早い習得につながります。
以下の本は参考になります。
『Excelで学ぶデータ分析本格入門』
一番大切な考え方『仮説思考』
やみくもにデータ分析をするのは、砂浜から一粒のダイヤを見つけるに等しい行為です。
過去の記事でも紹介しています。
まとめ
・データ収集方法
・エクセルでデータ基礎を見る
・エクセルで相関をみる
・エクセルで予測をする
・エクセル上級者を真似よう
を紹介いたしました。
予想通り、6月2週目でコロナ感染者0になるように、今は、「STAY HOME」を続けましょう。
私は災難が起こるたびに、これをよい機会に変えようと努力しつづけてきた。
ジョン・D・ロックフェラー(スタンダード・オイル社の創立者)
困難に勝る教育なし
ベンジャミン・ディズレーリ
私は未来は考えない。あっという間にやって来るからだ。
アルバート・アインシュタイン